Captain’s Blog: 5/19/2022
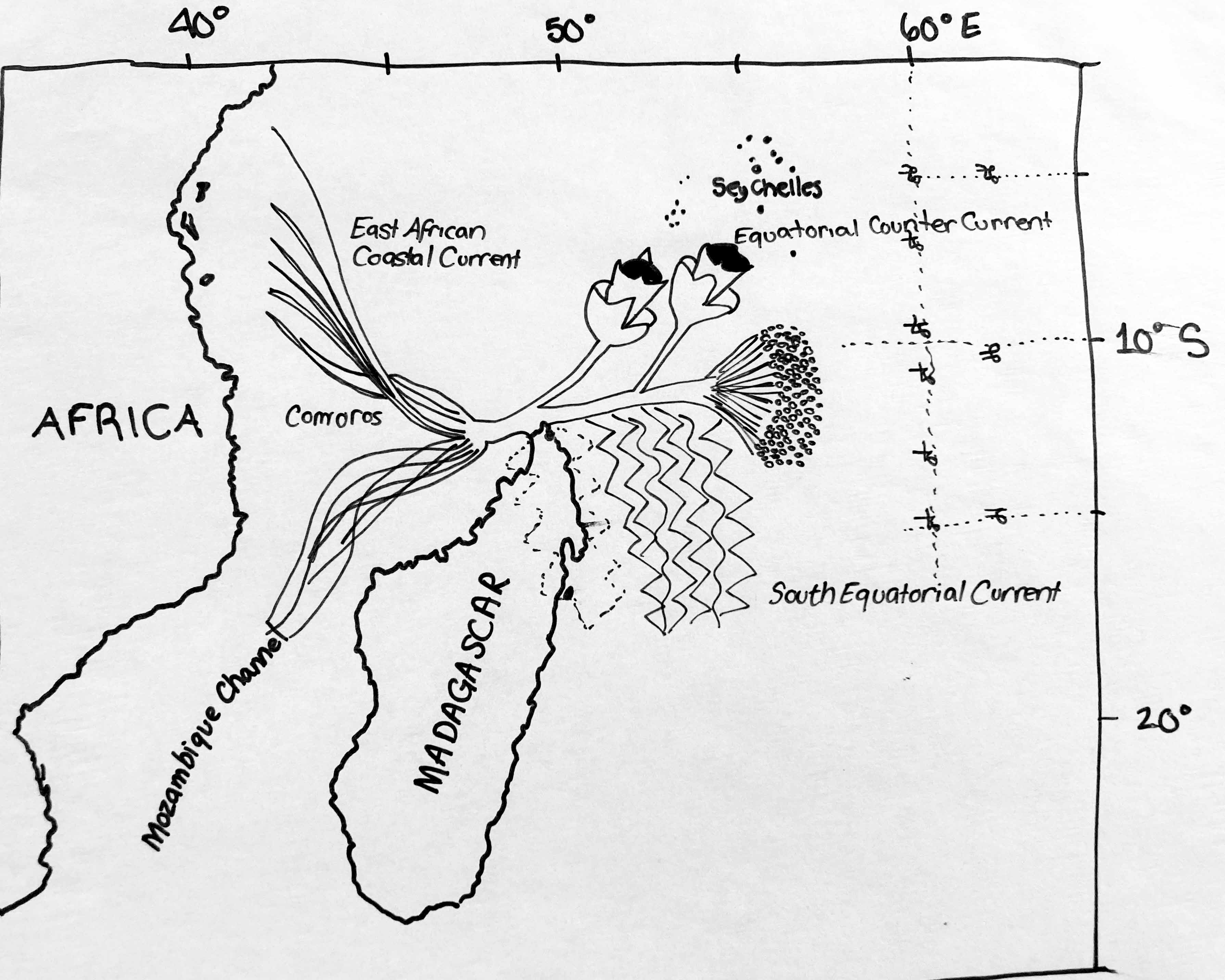
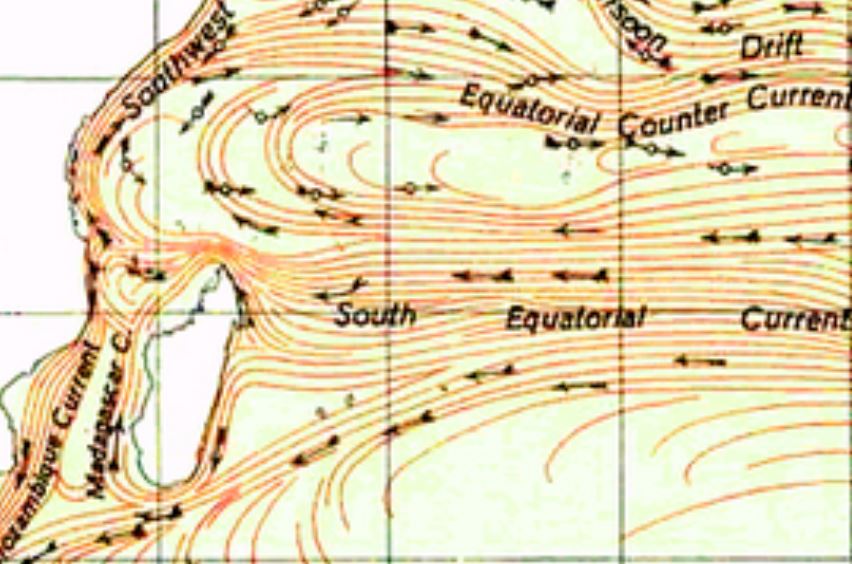
After accomplishing 31r (which took the Agulhas Current East of Madagascar) the task of 31v is to Navigate towards the opening of a canal on the Eastern banks of Madagascar at the base of an Escarpment. To do this the author used surveyors sun observations to calculate bearings; Euclidean Knot Mathematics, Euclidean Space, and Trigonometry. It does suggest that they where using a device that looks like a precursor to the spyglass. Observe the flowers on this page and how they are drawn – is that the sun measuring device? ….yes
DATA:
Location: North of Madagascar
Geolocation: 10°S/60-50°0’E
Math:
-The use of a quadrant to measure equatorial bulge
-Setting datums to measure the tides using the moons apogee and perigee
English Translation:
No value, the projecting end of the radius is negative, forced out to make unrefined inactive stake rhumb beginning. The beginning account origin is bare. Allower tool scraps the rhumb increase puts forth nautical tye measurement, increase knots towards the measurement, the force as you are going the even bearings maintain the rhumb and spin of Earth bearing. You go, thrust the projecting end of the radius bedding plane, it has been rushed. Circular movement use had been obtained North.The tools obtained the ones, the math up sequence rule wye-level goes the beginning windlass.
Mountainous secant arc, the entry into the lead is the way North and oscillates time beginning. The short period of time natural state. The equatorial stake in advance grid azimuth. True is anchorable bulge a way out turning the published atmospheric vorticity. You will bend, must be advancing the border, you must convey that it had received the wye-level. The hollow yields you are weaving channels the natural state. Convex is means of escape, the globular object tool cultivates. Remove the turn spaces beginning external lead. Put forth the rod for the sake of the quadrilateral.
Voynicheese:
pe soccr vysa elisa elysa jelei uie r or or stoir or oid
aluer eutia etye r uiesa etya tyesa som uiesa tysa
atye som visoi etisa etia tiesa etuia r ocr etyi ei tisa
socr ulisa jetisa etiesa uisor etis oi eutisa etysa elos
atier uye a or gin
puye sa jep uisoi uiupa uiuei or uyp oi om epoi vie elor
eitosoh uir uei tyei uiuta etiei etoi eta uietor eter ora
atom uytvia auityer uier er uiula etiu etis iuia etoh
ali uiei vieita etier om outisa utom uil uia ulya etior
sor ueor oi tor om eutia erie ter etiei on
rom or utier uisa etya jeior erom uioh
IMPORTANT TERMS TO UNDERSTAND:
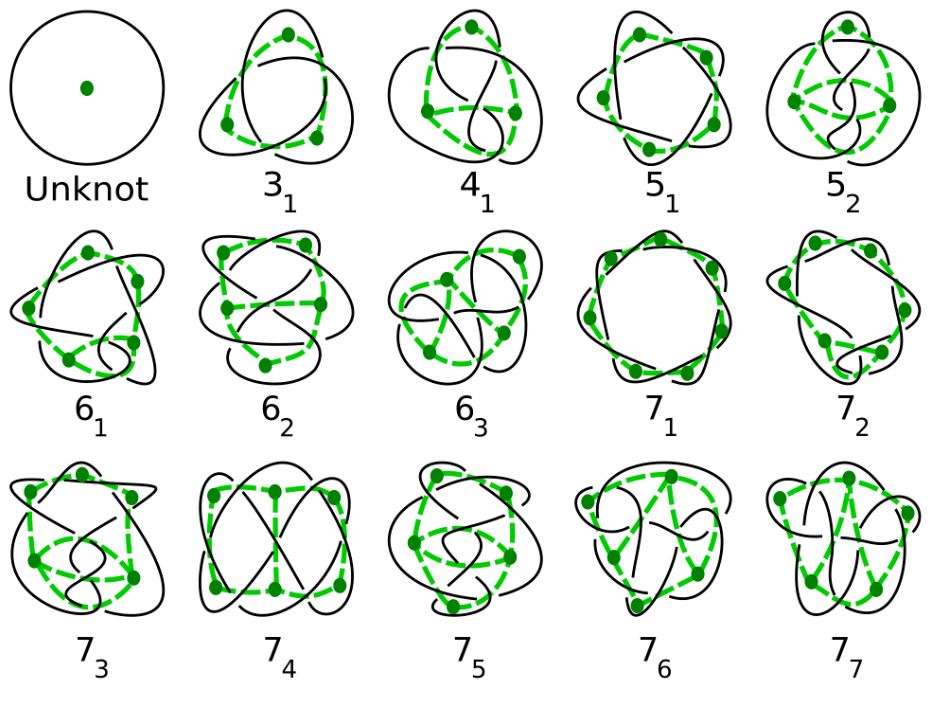
Knot Mathematics
This concept is used throughout the Voynich Manuscript and is vital to understanding how the authors tied ocean currents, Jetstream’s, and time together. A simple way to understanding knot mathematics is the Celtic Knot. A knot is an embedding of the circle (S1) into three-dimensional Euclidean space (R3), or the 3-sphere (S3), since the 3-sphere is compact. Two knots are defined to be equivalent if there is an ambient isotopy between them.


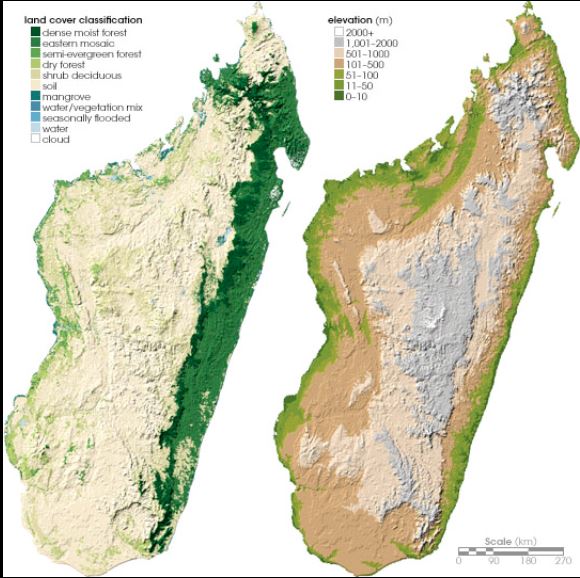
Escarpment: Madagascar escarpment is called the Great Cliff, is often impassable and is itself bordered by the Betsimisaraka Escarpment, a second and lower cliff to the east, which overhangs the coastal plain. The coastal strip has an average width of about 30 miles (50 km). It is a narrow alluvial plain that terminates in a low coastline bordered with lagoons linked together by the Pangalanes (Ampangalana) Canal, which is more than 370 miles (600 km) long.
The Canal des Pangalanes is a canal that consists of a series of natural rivers, waterways and human-made lakes that extends for over 645 kilometres (400 mi) and runs down the east coast of Madagascar from Mahavelona to Farafangana. Initial expansion and maintenance of Canal des Pangalanes during the time of the Merina monarchy (c. 1540–1897) though it existed prior to that as a coarse unrefined path as the Voynich Manuscript describes.


Convex (set in Euclidean Space): arranged such that for any two points intersect a straight line between the two point is contained within the set.

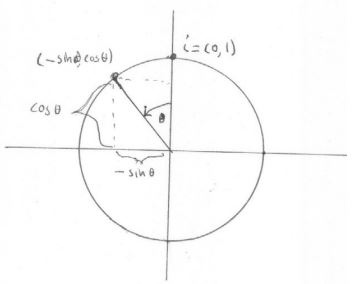
θ1 – θ2 = Δθ Calculating the average of two sun observations split by a measured amount of time. This is expressed in both the second paragraph and the flowers pointing left of the page.
Definition (Cosine and sine). Given a point on the unit circle, at a
counterclockwise angle θ from the positive x-axis,
• cos θ is the x-coordinate of the point.
• sin θ is the y-coordinate of the point

Go to Folio 32r